パレートの法則とは？一番わかりやすい入門編

みなさまはパレートの法則を知っていますか。「８：２の法則」などとも言われるパレートの法則は、さまざまなものごとに現れる分布の偏りのことです。パレートの法則を活用して、マーケティングや営業を効率化しましょう。

「利益を作る分析力がつく！ビジネスフレームワーク集25選」をダウンロードする

パレートの法則の概要

この章ではパレートの法則の概要をご説明いたします。

パレートの法則とは

パレートの法則とは「全体の数値の８割は、全体を構成する要素のうちの２割の要素が生み出している」という経験則のことです。

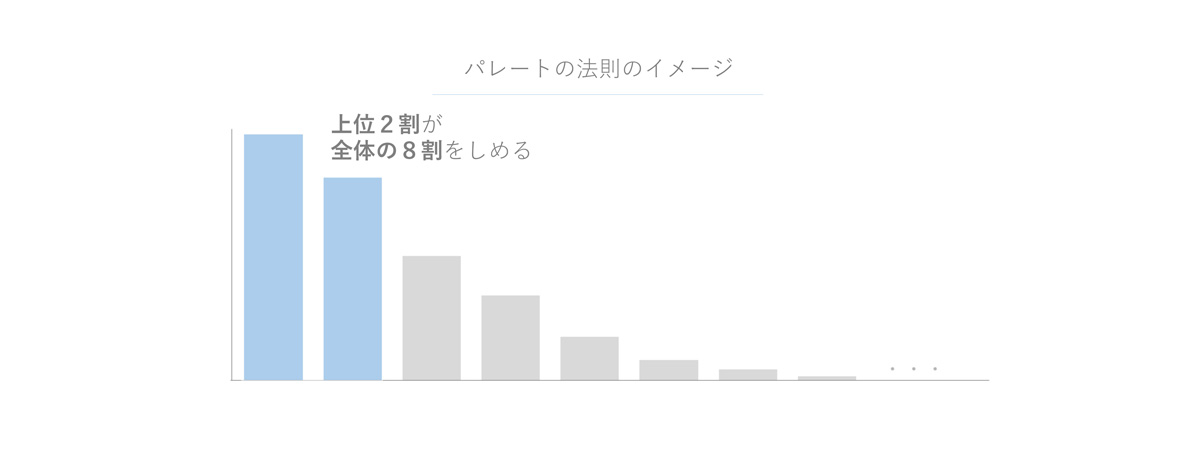
働きアリの法則や、ユダヤの法則もパレートの法則と似たような分布の偏りを表しています。あらゆるものごとは、パレートの法則と同様の分布の偏りがみられるといわれています。

パレートの法則は、ビジネスにも応用できます。パレートの法則をビジネスに応用するメリットは2つです。

1つ目は、リソースやコストの配分を効率化、最適化できることです。2つ目は、8：２の分布を仮説とし、とるべきマーケティング、営業施策を計画できることです。

パレートの法則をビジネスに応用する方法については、パレートの法則の活用例で詳しくご紹介します。

身近にあるパレートの法則の例

パレートの法則は身近にあふれています。みなさまの身近にある、パレートの法則の例をご紹介いたします。

• いつも着ている服の８割は、持っている服のうち、お気に入りの２割である
• 部屋で過ごす時間の８割は、部屋全体のスペースのうち２割の場所を使用している

パレートの法則の活用例

パレートの法則を活用することで、あるものごとの分布を予測できます。この予測から、マーケティングや営業の施策を立てることができます。仮説を持ちつつ、マーケティングや営業施策を立てることで、施策にかかるコストやリソースを最適化ができます。

手順１.パレートの法則を使ってあらかじめ、導かれる分布を予測する

あなたは新規事業の立ち上げを担当しているとしましょう。あなたが取り扱う製品の売上と顧客数は、どのような分布になるでしょうか。
パレートの法則にしたがえば、あなたの製品の売上のうち８割は、２割のお客さまによってもたらされると予想できます。
パレートの法則を用いて予測した結果、売上の８割をしめると思われる上位２割のお客さまと、下位８割にお客さまをセグメンテーションします。

手順２.予測した分布に合わせてマーケティング施策や営業手法を変える

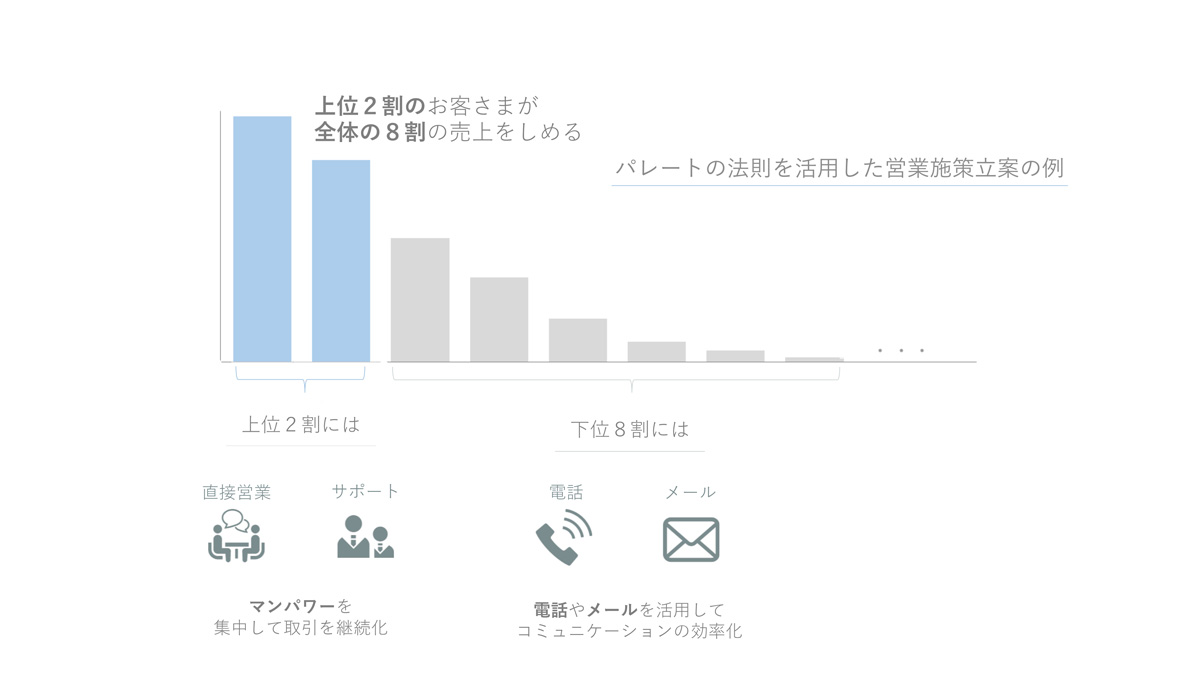
購買額上位２割のお客さまには、社内のマンパワーを集中させ、営業担当者が直接接触して営業する、ていねいなサポートを提供するなどします。
会社のリソースをパレートの法則の上位２割のお客さまに集中することで、上位２割のお客さまとの取引を、継続させることが目的です。
パレートの法則の下位８割のお客さまには、電話やメールなどを活用して、コミュニケーションにかかるコストを効率化しましょう。

パレートの法則の注意点

パレートの法則を活用する際には、以下の注意が必要です。

パレートの法則はあくまで経験則

パレートの法則は、論理や理論ではなく、あくまで経験則です。当然、パレートの法則とは異なる分布を示す場合もあります。

では、パレートの法則は役に立たないのでしょうか。そうではありません。

「パレートの法則のように、分布に偏りがある場合がある」ことを知っていれば、「もしかしたら分布に偏りがあるかもしれない」という仮説に基づいて、分布の分析や施策の立案を行うことができます。

分布を分析する際に、ゼロベースから網羅的に情報を集めて、膨大な情報の中から何らかの傾向を見出すのは、簡単ではありません。

しかし、パレートの法則を知っていれば、「もしかしたら分布に偏りがあるかもしれない。本当だとしたら、〇〇の施策が有効なのではないか」と仮説を立てることができます。

パレートの法則はあくまでも経験則です。鵜呑みにするのは危険が伴います。パレートの法則を活用する際は、「パレートの法則を足がかりに、あらかじめ仮説や施策を考える」くらいにとどめておきましょう。

下位８割は不要、とは限らない

たとえば、とある10人の営業部があったとします。その営業部では、売上の８割を成績上位2人の担当者が生み出しています。

この場合、２割の売上しか生み出さない８人の営業担当者は、全員サボっているのでしょうか。

下位８人の営業担当者をクビにしたとしても、成績上位２人の営業担当者はこれまで通りの結果を出せるでしょうか。

そうは言いきれません。

組織の中では、互いに補い合い、サポートし合います。成績上位2人の結果も、下位８人の担当者に支えられてこその結果かもしれません。

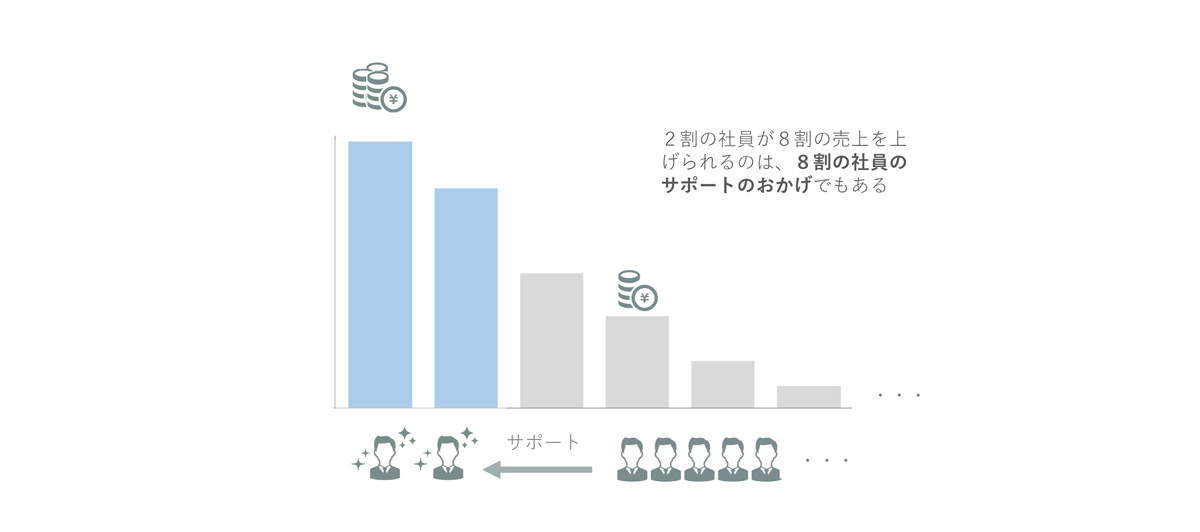
パレートの法則の分布において、２割の結果しか生み出さない下位8割の存在が不必要とは言い切れないのです。